
Mass balance equations facilitate understanding of the quality of food by determining the different food components and how they complement each other.
The various components of milk are often expressed as a percentage of the total, usually based on 100 grams sample. These components can also be expressed in terms of grams of the component per gram of the food sample by dividing the component value by the total sample size (100 g).
In a mass balance equation, it is very important to determine the moisture component of the food sample to facilitate further analysis of the dry matter.
Eliminating the moisture content from the sample is necessary because it allows for convenient expression of the fractional compositions of the various components in the solid food sample.
Consider the table below for a proportional analysis of a milk sample
|
Constituent |
Content (% of total mass) |
|
Water |
87.6 |
|
Butter fat |
3.8 |
|
Protein |
3.2 |
|
Lactose |
4.6 |
|
Ash |
0.7 |
With reference from the table above, how much of this milk should a person drink to obtain 64 grams of protein?
Say the amount of milk is M kg
Then, 0.032M = 64
M = 64/0.032
M = 2000g or 2 kg
Natural law states that matter/mass can neither be created nor destroyed; it can only be changed into various forms and shapes. Such can either be an agglomeration into larger mass or breakdown into smaller pieces.
Passing a given mass of substance through a system produces a product of an equal mass as the raw materials fed into the system, provided no mass is stored in the system (losses).
Given that foods have to be mixed to achieve a recommended nutritional balance, the individual components may vary in the output.
However, the mass of the individual components into the system will always remain equal to the sum out of the system given that the system does not retain any piece.
Understanding the concept of mass balance equations lay the foundation for mass balancing, which is the basis for food formulation, designing system capacities, and auditing of the process plant materials.
One constituent mass balancing involves the concentration of foods by evaporating water. In this case, it is assumed that only the water evaporates from the food and never the dry matter.
Consequently, the mass balancing for such a system can be represented as indicated in the figure 1 below:
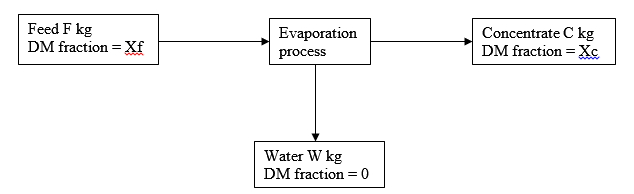
From the diagram,
Total mass balance (TMB): T = C + W
Dry mass balance (DMB): FXf = CXc + WXw
Given that Xw = 0;
It follows that FXf = CXc
Therefore; C = FXf / Xc
And W = F – C
If we concentrate 200 kilograms of milk with a composition indicated in table 1 above to 25% dry matter content, how much concentrated milk is expected assuming no process losses and how much water will be evaporated?
TMB: 200 = C + W
DMB: 200*0.124 = 0.25C + 0
Therefore; C = (200×0.124) / 0.25 = 99.2 kg
Amount of concentrated milk expected from the process is 99.2 kg
Amount of water to be evaporated = 200 – 99.2 = 100.8 kg
A scenario where a product loss occurs:
If we concentrate 200 kg of milk with composition from table 1 to 25% dry matter content, how much concentrated milk would be expected if there is a 3% loss on the process and how much water will be evaporated?
TMB: 200 = C +W
DMB: 200×0.124 = 0.25C +0
Therefore; C = (200×0.124) / 0.25 = 99.2 kg
However, there is 3% product loss, so we have 97% efficiency
Meaning, C = 0.97×99.2 = 96.224 kg
Amount of water to be evaporated remains the same; W = 200 – 99.2 = 100.8 kg
Flavors in foods are as a result of volatile compounds, which are mostly lost during the evaporation process. The loss in these volatile compounds may lead to serious sensory quality problems, especially in a fruit juice manufacturing process.
The problem of flavor loss in fruit juice processing is countered by over-concentrating one portion of the juice and then diluting with a fresh portion to compensate for the lost flavor.
Typically, a mass balance of the manufacturing process in a fruit juice processing plant can be represented schematically using figure 2 below:
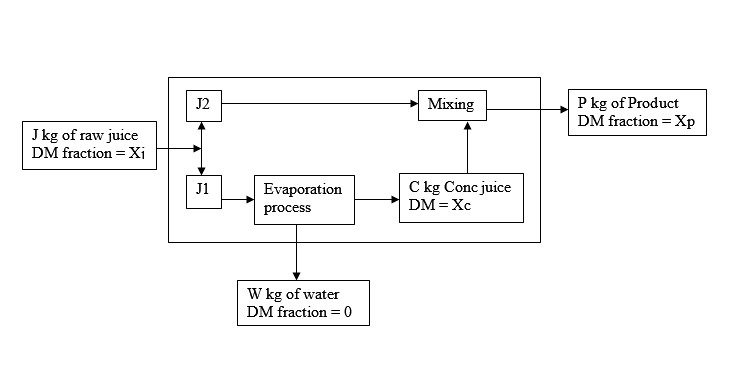
From the diagram, consider that the overall process uses J kg of raw juice to produce P kg of the final produce and W kg of water.
The mass balance equations for the process
TMB: J = P + W
DMB: JXj = PXp
Meaning that P = JXj / Xp
And W = J – P
Consider mixing J2 and C to form P using the value of P obtained from the previous step
Therefore, the mixing process looks like this:
TMB: P = J2 + C
DMB: PXp = J2Xj + CXc
Meaning C = (PXp – J2Xj) / Xc
And J2 = (PXp – CXc) / Xj
Consider the evaporation process whose equations become:
TMB: J1 = C + W
If there is any loss of product in the process, the final yield can now be calculated using the values from the three equations.
In the production of mango juice concentrate, 1500 kg of raw juice with 12% dry matter content is first subdivided into two.
The first portion is concentrated to 55% dry matter content, which is then diluted with raw juice to make the final product with 45% dry matter content.
During processing, there is a 4% loss incurred. Calculate the amount of juice in each portion, the expected product and the amount of water to be evaporated.
With reference to the figure 2 above, we can develop the schematic flow of the process.
What we already know; J = 1500, Xj = 0.12, Xp = 0.45, Xc = 0.55
TMB: 1500 = P +W
DMB: 0.12×1500 = 0.45P
Therefore, P = (0.12×1500) / 0.45 = 400 kg
Amount of water to be evaporated, W = 1500 – 400 = 1100 kg
TMB: 400 = J2 + C
DMB: 0.45×400 = (0.12×J2) + 0.55C
Solving for C gives 307 kg and J2 gives 93 kg
TMB: J1 = 307 + 1100 = 1407 kg
Amount of product expected, Pactual = 0.96×400 = 384 kg
J = J1 + J2 = 1407 + 93 = 1500.


Comments