Milk Standardization: How to Use the Pearson’s Square Method

Milk standardization is important in the dairy industry because it is used to ensure that every consumer gets milk with constant fat content and consistency. Primarily, milk may be separated into two products; cream with high fat content (about 40% fat) and skimmed milk (about 0.03% fat) using a centrifugal separator.

You can separate milk into cream (40% BF) and skimmed milk (0.03% BF) using a centrifugal separator. Click To Tweet

The process of standardization involves reduction of fat content in milk from the natural minimum of 3.25%. The cream extracted from the standardization process facilitates processing of other dairy products such as ice cream, butter, and ghee.

Milk standardization can take two forms i.e. either partial separation or mixing of skimmed and whole milk. Mass balancing plays a key role in successful standardization of milk.

Example 1

2000 kg of milk (with 87.6% water, 3.8% fat, 3.2% protein, 4.6% lactose, and 0.7% ash content) has to be reduced in fat content from 3.8% to 2.5% by removal of cream with 40% fat content from the milk. How much milk will have to be removed?

Solution.

TMB: 2000 = C + M

FMB:   2000*0.038 = 0.4*C + 0.025*M

2000*0.025 = 0.025*C + 0.025*M

Solving the equations will give the values of C = 69.3 kg and the remaining milk M = 1930.7 kg.

Example 2

If 3000 kg of the same milk used in the previous example is separated into cream with 45% fat and skimmed milk with 0.05% fat, how much cream and skimmed milk are expected assuming no losses?

Solution

TMB:   3000 = C + M

FMB:   3000*0.038 = 0.45*C + 0.0.0005*S

Solving the equations will give C = 250.3 kg and S = 2749.7 kg

See also: Mass Balance Equations: Standardizing Juice Concentrates

Consider mixing W kg of whole milk with a fat content of fw and S kg of skimmed milk with a fat content of fs to obtain X kg of standardized milk with fx.

There is only one value, pw, for the fraction of W in X and one value, Ps = (1-Pw) for the fraction of S in X.

The challenge to the processor is to determine these values.

Using mass balance:

TMB:   W + S = X, and W + S = W + S

FMB:   Wf_w + Sf_s = Xf_x

Xf_x = f_x(W + S)

Expanding the equations

Wf_w + Sf_s = Wf_x + Sf_x

W(f_w – f_x) = S(f_x – f_s)

W/S = (f_x – f_s)/(f_w – f_s)

W/(W + S) = (f_x – f_s)/[(f_x – f_s) + (f_w + f_s)] = P_w = W/X

S/(W + S) = (f_w – f_s)/[(f_x – f_s) + (f_w – f_s)] = P_s = S/X

NB: (f_x – f_s) + (f_w – f_s) = (f_w – f_s).

Milk Standardization Using Pearson’s Square Method

Due to the complexity of the equations above, the Pearson’s Square method was developed. The square is drawn and then the immediate constituent content is placed at the center, which in this example is f_x.

The Pearson Square simplifies the mass balancing process during food standardization. Click To Tweet

Place the higher constituent content (f_w at the left hand side top corner and the lower constituent content at the left hand side bottom corner). Subtract diagonally the higher value from the smaller value as illustrated in the figure below.

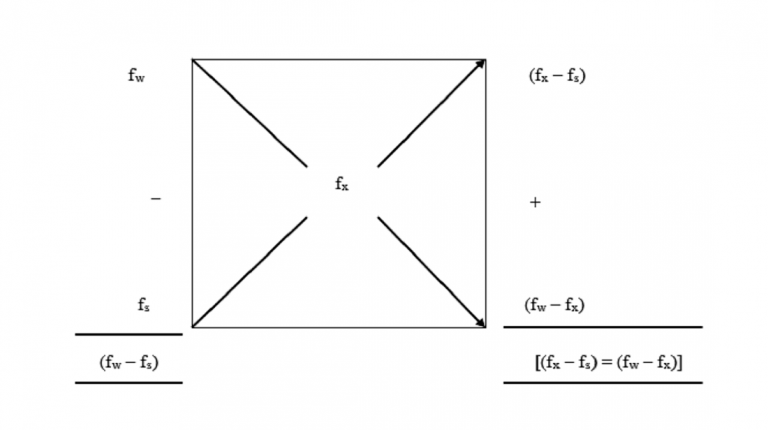
Please note that the sum of the values on the right hand side of the square equals the value at the top left minus that at the bottom left side and this value represents X.

The value at the top right represents W and the value at the bottom right represents S. From the values, you can calculate the proportions of W and S, Pw and Ps respectively in X.

The Pearson’s Square is ideal for use when you have to use two streams/substances to standardize one constituent.

Example 3

How much whole milk with 3.9% fat and skimmed milk with 0.04% fat content will you need to produce 2000 kg of standardized milk with 2.5% fat?

Solution:

Using mass balance method:

TMB:   W + S = 2000

FMB:   0.039*W + 0.0004*S = 0.025*2000

Solving for W = 1274.6 kg and S = 725.4 kg

Using Pearson’s Square method:

Proportion of the whole milk = 2.46/3.86

Amount of whole milk required = (2.46/3.86)*2000 = 1274.6 kg

Proportion of skimmed milk = 1.4/3.86

Amount of skimmed milk required = (1.4/3.86)*2000 = 725.4 kg (or 2000 – 1274.6)

Milk Standardization: Mass Balancing of Two Constituents in Food

Energy in Food

Nutritionally, energy from food is expressed in calories (Cal) or kilocalories (kCal). One calorie is the amount of heat energy required to raise the temperature of one gram of water by 1°C, say from 10°C to 11°C. This heat energy is equivalent to 4.1868 Joules. 1000 kCal is the amount of heat energy needed to raise the temperature of 1 kg of water by 1°C or 4186.8 J (4.1868kJ).

Body energy comes from fats (with 9kCal/g or 37683kJ/kg), carbohydrates (with 3.75kCal/g or 1570kJ/kg), and protein (with 4kCal/g or 1674kJ/kg).

Nutritionists express the nutrient and energy content of food as the amount contained in 100g of the food. Energy to protein ratio, expressed as kilocalories per gram of protein is an important nutritional quality aspect in food. Based on the composition and energy content, the nutritional content of food can be determined and expressed.

Protein Energy Ratio Calculation

The energy to protein ratio of food is used to define the nutritional quality of food. The recommended energy to protein ratio in human diet is approximately 40kCal/g protein (16742kJ/kg protein).

Example 4

Calculate the energy to protein ratio of milk given the composition of the sample is 87.6% water, 3.8% fat, 3.2% protein, 4.6% lactose, and 0.7% ash content.

Solution

Nutritional language:	Constituent	Content in 100g	Energy contribution (kCal/100g)
	Fat	3.8	3.8*9 = 34.2
	Protein	3.2	3.2*4 = 13.8
	Lactose	4.6	4.6*3.75 = 17.25
Total			65.25
Energy to protein ratio = 65.25/3.2 = 20.4kCal/g protein
SI Engineering units:	Constituent	Content (fraction)	Energy contribution (kJ/kg)
	Fat	0.038	0.038*1*37683 = 1432
	Protein	0.032	0.032*1*16748 = 535.9
	Lactose	0.046	0.046*1*15701 = 722.2
Total			2690.1
Energy to protein ratio = 2690.1/(0.032*1) = 84065.6kJ/kg protein

 

If you have to mix two ingredients in amounts of W and M (g) respectively so that the resulting mix has a stated energy to protein ratio, Rp, then one ingredient must have a greater ratio and the other smaller than the desired. Once you have selected, you can use the following equations to determine the proportions of the ingredients for the mix.

TMB:   W + M = P

R_p = (We_w/Wp_w) + (Me_m/Mp_m) = (Pe_p/Pp_p)

Where, e is the energy content and p is the protein content and the subscripts w and m represent ingredients W and M respectively.

Example 5

Assume you have the following foods and their composition

Ingredient	Composition per 100g
	Protein content	Energy content
Whole milk powder	27	530
Millet flour	6.7	330
Soybean flour	40	433

 

Using the information above, prepare a recipe for a 500kg mix containing 40kCal per gram of protein.

Solution.

Required energy/protein for the product,       R_p = 40/1 = 40kCal/g

Energy/protein for whole milk powder,          R_w = 530/27 = 19.6kCal/g <R_p

Energy/protein for millet flour,                        R_m = 330/6.7 = 49.25kCal/g >R_p

Energy/protein for soybean flour,                 R_s = 433/40 = 10.8kCal/g <R_p

Thus a mixture of either millet and milk powder or millet and soybean flour can be used.

Using a mixture of W g of whole milk powder and M g of millet,

TMB:   W + M = P

R_p = (530*W/27W) + (330M/6.7M) = 40/1

530W + 330M = 1080W + 268M

550W = 62M

W/M = 62/550

W/(W + M) = 62/612 = W/P

M/(W + M) = 550/612 = M/P

To prepare 500kg of the mix, amount of whole milk powder required, W = 500*(62/612) = 50.7 kg and the amount of millet flour, M = 500*(550/612) = 449.3 kg.

To verify the credibility of these figures,

R_p = (50.7*530 + 449.3*330) / (50.7*27 + 449.3*6.7) = 40

Example 6

Given whole milk powder, soybean flour and millet, prepare a recipe for 350 kg of a mix with 40 kCal per gram protein, which contains equal protein from soybean and whole milk powder.

Solution

From the constitution, it is not hard to deduce that 27g of soybean has the same amount of protein as 40g of whole milk powder and the amount is 27*0.4 = 40*0.27.

To begin with, we need to formulate a mixture of soybean flour and whole milk powder as given above and determine its composition.

Its energy content will be, e_x = [(27*433 + 40*530) / (27 + 40)] = 490.9 kCal/100g

Its protein content will be, p_x = [(27*40 + 40*27) / (27 + 40)] = 32.2 gprotein/100g

Energy to protein ratio of the mix, p_x = 490.9/32.2 = 15.24 < 40 hence you can mix it with millet flour to obtain the required energy to protein ratio.

TMB:   X + M = 350

R_p = (491*X/32*X) + (330*M/6.7*M) = 40/1

491M + 330M =1280X + 268M

789X = 62M

X/M = 62/789

X/(X + M) = 62/851 = X/P

M/(X + M) = 789/851 = M/P

Amount of mix, X = (62/851)*350 = 25.5 kg

Amount of millet, M = 350 – 25.5 = 324.5 kg

In the mix;

The amount of whole milk powder, W = (25.5*40) / 67 = 15.2 kg

The amount of soybean flour, S = 25.5 – 15.2 = 10.3 kg

The final recipe is thus, 324.5 kg millet, 15.2 kg whole milk powder, and 10.3 kg soybean flour.